The Rust language has shown that there are interesting points in the space of possible memory management strategies that haven’t been explored. Most memory management approaches can be categorized as manual, garbage collected, reference counted, or region based. But other options and combinations are possible. The Lobster language is exploring a unique combination of reference counting and compile-time analysis. The “As Static As Possible” approach described by Proust is also interesting.¹ His paper also does a good job of describing the other memory management approaches and placing them in one possible space of categories. I’ve been exploring the space of compile-time memory management (CTMM) approaches for use in the Adamant language. It will have CTMM similar to Rust, but is meant to be easier to use. One of the most interesting and potentially useful ideas I’ve found is that of combining compile-time memory management with a bit flag for ownership. Something I’m calling potentially owning references.

Potentially Owning References

Each language with CTMM has its own variation on the idea. In general though, they have owning references and borrowed references. An owning reference is one that owns the object it references and is responsible for deleting it. When an owning reference is passed to or returned from a function, there are no other references to the object. The owing reference is a unique reference. Owning references can be safely deleted or put into longer-lived objects. There is no risk that another reference will become invalid or delete the object. Within a function, additional references can be created to the same object as an owning reference. These borrowed references are temporary aliases of the owning reference. The compiler then ensures that all borrowed references are gone before the owning reference can be deleted or given away. For many functions and fields it is clear that each reference should either be owning or borrowed.. But sometimes, the caller would like to determine which way a function is used. Potentially owning references enable this by creating another reference type that acts as a hybrid of an owning and borrowed reference.

A potentially owning reference carries with it a one-bit flag which indicates whether that reference has ownership of the object. If the reference has ownership, then it will need to be handled like an owning reference and deleted. If the reference is borrowed, how long it exists may need to be limited to keep memory safe. Consequently, potentially owning references have the limitations of both owning and borrowed references enforced on them by the compiler. Any borrowed references created from it must be gone before it can be deleted or given away. Of course, when it would be deleted, the language inserts a check that deletes it only if the ownership flag is set. Since the reference could actually be borrowed, it must be treated as potentially being bounded by the owning reference it was borrowed from. A potentially owning reference stored into an object will require the lifetime of that object to be limited by the lifetime of the reference. Of course, the caller of a function doing that may know that the reference is owning and therefore, no limit is placed on the object.

Examples

Consider the implementation of an immutable string type. It will hold an immutable array of Unicode characters (codepoints). Many string objects will own the array they hold. However, to avoid constantly making copies of the string data, we’d like to be able to share the character array between strings. For example, when we take a substring of a string, it would be ideal if we didn’t have to copy the characters but could borrow a reference to the character array and use an offset and length to track which slice of that array was the current string. In that case, the array reference should be borrowed. We could implement this with two different subclasses of string. One subclass for regular strings that own their character array and another subclass for strings that borrow their character array. That would be a lot of code duplication and complexity. Instead, we can use a potentially owning reference. If that was done, the string class data could be declared like this.

public class String
{
    public let length: size;
    let start: size;
    let data: uni Array[codepoint]; // potentially owning reference
}

This example uses the keyword uni, an abbreviation for “unique”, to mark the character array as a potentially owning reference. This may not be the keyword used in the final version of the Adamant language. It was chosen because even though such a reference could actually be borrowed, the developer may generally treat it as if it were an owning reference. However, it isn’t. So to avoid confusion, another word is needed. The word “unique” conveys that the reference can be treated as if there were no other references to the same object without directly implying ownership. It should also be noted that, in Adamant, arrays directly support slicing, and strings are implemented more efficiently using structs. This example is written to explain potentially owning references clearly.

With the string fields declared this way, we can create new strings that own their data. For example, the append method returns a new string that owns a new character array. The method return type uni String indicates that it returns a potentially owned string object. It is not about the type of the character array inside that object.

public fn append(self, other: String) -> uni String
{
    let newLength = .length + other.length;
    let newData = mut new Array[codepoint]();
    .data.copy_to(newData, .start, 0, .length);
    other.data.copy_to(newData, other.start, .length, other.length);
    return new String(move newData, 0, newLength);
}

The String class also allows for borrowed string data. For example, the substring method returns a new string that borrows the character array of the source string. The method return type uni String <~ self indicates it returns a potentially owned string object whose data may be reachable from the object self. The returned string needs to be deleted before the self string to ensure memory safety. (See the previous post for a full explanation of reachability annotations.)

public fn substring(self, start: size, length: size)
    -> uni String <~ self
    requires start + length <= .length
{
    return new String(.data, .start + start, length);
}

Potentially owning references combined with immutable references allow for even more flexibility. Consider the declaration below of a string constant. The character data for that string should be stored once in memory. A new array shouldn’t be allocated each time this code is run. It is safe to assign constant data to immutable potentially owning references. Since they are immutable, it is impossible for someone to mutate the constant data through them. Since they can borrow data, it won’t attempt to delete the constant data.

let example: const String = "This is my string.";

Compile-Time vs. Runtime

I said Adamant used CTMM, but potentially owning references rely on a flag that must be passed with the reference and checked before deleting the object they reference. Does that mean they shouldn’t count as CTMM? To me, the purpose of CTMM is to provide safety and efficiency in memory management. Today most popular languages rely on the purely runtime memory management of garbage collection. Yet, garbage collection is a hack. At the moment it is a very necessary hack that makes programming much more enjoyable and productive. I don’t think programming languages a thousand years from now will use garbage collection. Language designers will have figured out memory management strategies that use compile-time rules possibly combined with some runtime tracking in a way that elegantly manages memory efficiently with little added burden to the programmer. That is the direction new CTMM languages should be headed in. It is fine if some runtime operations are needed, as long as those are efficient and elegant. Indeed, Rust, the poster child for CTMM languages, sometimes needs drop flags to handle function bodies with code paths that conditionally drop references.

Implementation

Potentially owning references can be implemented fairly simply and efficiently on modern hardware. The ownership flag needed is not a property of the object itself. Different potentially owning references could refer to the same object, and only one of them will have ownership of that object. A flag must be stored with each reference. How can that be done efficiently? It is important to remember that CPUs are now much faster than memory access, so a few extra instructions needed to access memory won’t have much impact. Potentially owning references can be implemented using tagged pointers. Assuming all object pointers are aligned to two-byte or larger memory boundaries, the lowest bit of a pointer will always be zero. The lowest bit can then be used to store the ownership flag. This allows the flag to be passed to functions and stored in objects as part of the pointer without any additional memory or operations. When dereferencing such a pointer, the bottom bit can be masked off before memory access. That is a single extra non-branching instruction before accessing memory. When objects should be deleted, the delete is conditioned on the bottom bit of the pointer.

A Starting Point

Designing a new CTMM strategy is challenging. Taking existing designs and altering them slightly tends to produce invalid, unsafe approaches. Finding a new one requires simultaneously changing multiple things to produce a new consistent design. Potentially owning references enable a new degree of flexibility in CTMM by allowing a function or object to either borrow or take ownership of a reference. While they are only a single piece of the puzzle, potentially owning references could be the foundation of another important approach to memory management in programming.

Rust’s lifetime annotations are one of the more confusing features of the language. It’s planned that Adamant will use a memory management strategy similar to Rust’s. However, Adamant needs to be easier to use. As such, I’m working hard to come up with a better alternative than lifetime annotations for Adamant. That could be just an easier or clearer syntax for the same thing or a radical rethinking of how reference lifetimes are handled at function calls. The latest incarnation of those ideas is what I’m calling reachability annotations.

The original Adamant language specification contained something very similar to Rust’s lifetime annotations except with different operators and the ability to inline the constraints next to the variable types. A refinement of that was described in the first blog post about memory management in Adamant as lifetime constraints. From there, the design evolved into “A New Approach to Lifetimes in Adamant”. It was based around which parameters’ lifetimes went into creating the return value. But, sometimes, that isn’t sufficient. Lifetime constraints can still be needed. Reachability annotations are the next step in the design evolution.

Rather than describing lifetimes and their relationships, reachability annotations indicate which objects might be directly or indirectly referenced by another. For the moment, the syntax for this is the reachability operator ~>. Given two variables, x and y, the expression x ~> y would indicate that y is potentially reachable from x. There are two ways that could be the case. Either the variable x could directly reference the object referenced by y, or x could reference an object which referenced the object referenced by y. Of course, there can be more levels of indirection. Any object reachable by following a series of references from x could be the one referencing y. Reachability annotations aren’t just for variables. They mostly appear in types. Given some type T, the type T ~> y is the type of things with type T that might reference directly or indirectly the value of the variable y.

Stating reachability annotations can be awkward. I haven’t found an easy way to read x ~> y without reversing it to “y is reachable from x”. Thinking about the graph formed by objects and their references to each other can be helpful. Then each object defines a subgraph composed of all the objects reachable from it. The reachability operator indicates that the subgraph of the first object may include the subgraph of the second object. To get a better understanding of this, we’ll work through some examples.

Annotations on Return Types

The primary place reachability annotations are needed is on return types. Within the body of a function, the compiler can infer reachability. When calling another function, the compiler couldn’t infer reachability unless it were to analyze the program as a whole. That can be slow. It can also lead to unexpected behavior as the implementation of one function can affect the inferred reachability in another. Without fixed reachability on function return types, a change to the implementation of a function could break backward compatibility in unobvious ways.

For ease of comparison, I’ll continue to use the same example I used in my previous posts. A function that takes two strings and returns the longer of the two. This is straight forward to think about with reachability annotations. The returned reference could reference either string passed to the function. To annotate that something could reference multiple things, we list them separated by commas.

public fn longest(x: String, y: String) -> String ~> x, y
{
    return if x.grapheme_count() > y.grapheme_count()
                => x
           else
                => y;
}

The highlighted code expresses that the returned String reference could reference the value of either x or y. Of course, it can’t reference both. The reachability operator is not a promise that something will be referenced. Instead, it indicates something may be referenced.

The longest function is a simple example, but more complex reachability type annotations are possible. In these examples, note that Tuple is a value type while List[T] is a reference type. Consequently, the list reference must be annotated with the owned reference capability. This indicates that the caller of the make_list function has ownership of this list, and it will be deleted when they are done with it. If you’re familiar with previous versions of Adamant, you’ll notice that ownership used to be a lifetime, but is now a reference capability. With the switch to reachability annotations, the concept of a lifetime doesn’t make as much sense anymore.

public fn make_tuple(x: String, y: String)
    -> Tuple[String ~> x, String ~> y]
{
    return #(x, y);
}

public fn make_list(x: String, y: String)
    -> owned List[String ~> x, y]
{
    return #[x, y];
}

Parameter Reachability Annotations

Some functions mutate their parameters. When that happens, it is necessary to annotate the function with the possible change in reachability. Consider the assign_into function, which takes a string and a reference to a variable of type String and assigns the string into the variable using the dereference operator ^. For this to be allowed, we must declare that the string may be reachable from the referenced variable after the function returns. This is a side effect of the function and is annotated as an effect using the may keyword.

public fn assign_into(value: String, variable: ref var String)
    may variable ~> value
{
    ^variable = value;
}

“Reachable From” Annotations

Up to this point, we’ve looked at annotations indicating which objects may be reachable from a reference. However, sometimes, the important information is what objects may reference the object in question. Methods often return objects that are still referenced by the object the method was called on. This needs to be annotated so the compiler can correctly manage the memory of such objects. This is done using the reverse reachability operator <~. An expression x <~ y can be read, “x may be reachable from y”. In the example below, this is used to indicate that the Tire object returned from the oldest_tire method could still be referenced by the Car object.

public class Car
{
    public let model_year: Year;
    public let tires: owned List[Tire];

    // the special parameter "self" is like "this"
    public fn oldest_tire(self) -> Tire <~ self
    {
        return .tires.order_by(fn(t) => t.replaced_on).first();
    }
}

One could imagine writing the return type of the oldest_tire method as self ~> Tire. However, that would make types difficult to read because one wouldn’t know if the type name came first until finding the reachability operator. Using the reverse reachability operator ensures the type comes first. For readability, the Adamant language requires that in a reachability expression between a type and a variable, the type must appear on the left-hand side.

Reachability in Classes

One area where reachability annotations need further development is when dealing with complicated relationships between the fields of classes. When a lifetime annotation would be required on a struct in Rust, how is that handled with reachability annotations? In the previous version of Adamant, this was handled by introducing named lifetimes as part of the class, similar to associated types. Something similar may be required with reachability annotations. Alternatively, if those correspond to specific fields, then it may be sufficient to indicate that those fields have separately tracked subgraphs. The example below shows one possible syntax for that.

public class Context
{
    public let text: ~> String;

    public new(.text) {}
}

public class Parser
{
    public let context: ~> Context;

    public new(.context) { }

    public fn parse(self)
        -> Result[never, String ~> context.text]
    {
        return Error(self.context.text.slice(1..);
    }
}

public parse_context(context: Context)
    -> Result[never, String ~> context.text]
{
    return new Parser(context).parse();
}

Here the reachability operator is used as a unary prefix operator to indicate that the field name can be used to refer to the subgraph reachable from that object. Then the member access operator is used within reachability expressions to refer to these subgraphs. Thus the parse_context function can express that the context will not be reachable from the return value, but the context’s text may be.

Next Steps

Reachability annotations need further work. Reachability in classes isn’t well developed and may need a better syntax. Reachability annotations may be confusing when used with mutable variables. It also isn’t clear how memory management compiler errors can be clearly expressed when using reachability annotations. In Rust, such errors refer to the lifetime of various references. With reachability annotations, the concept of a lifetime doesn’t exist in the syntax of the language. There is only reachability. Can error messages be clearly stated in terms of reachability?

Despite the work still needed, reachability annotations seem like a good step forward toward creating a more developer-friendly version of compile-time memory management. They are mostly isomorphic to the previous approach taken by Adamant. Thus I’m confident they can be made to work. Yet, I think they are much easier for the developer to think about and reason about. Even if Adamant isn’t able to develop this idea into a production language, hopefully reachability annotations can be an inspiration for other languages.

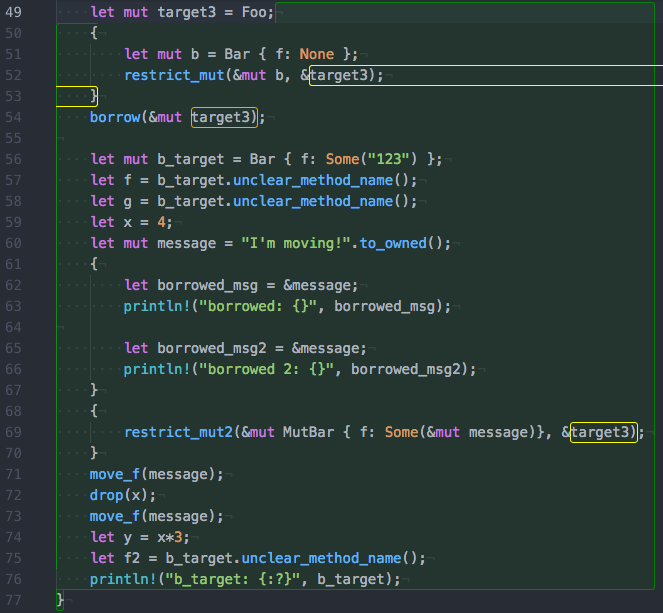
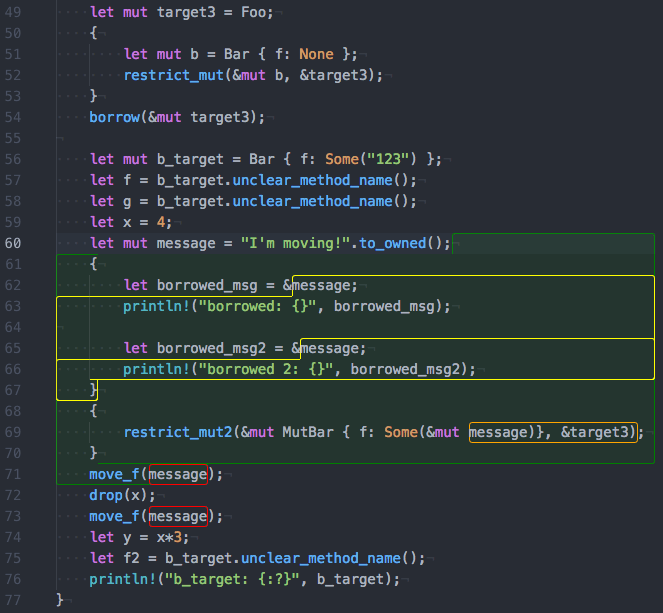
Trying to design a new programming language, I’m faced with the question of how to implement a parser for it. Various parser generators are available and support a soup of parsing algorithms including LL, LR, LALR, ALL(*), GLR, and others. Ideally, I could look at the parser generators for the language I’m working in and pick the one that suited my use case. Unfortunately, despite a lot of searching, I’ve never found one that works well for language design or for that matter production compilers. Instead, I’ve ended up implementing a recursive descent parser that switches to precedence climbing for expression parsing. Approaches like that are prevalent in both the programming language design community and production compilers. If computer science has extensively studied parsing algorithms and many parser generators have been written, how come they aren’t used? Indeed, parsing is often treated as if it is a “solved problem.” What gives?

I’m not the first person to notice this contradiction. In “Parsing: The Solved Problem That Isn’t” (2011), Laurence Tratt survey’s the algorithms available and explains why he finds them inadequate. Likewise, Parr and Fisher open their paper “LL(*): The Foundation of the ANTLR Parser Generator” (2011) by saying “Parsing is not a solved problem, despite its importance and long history of academic study.” Then again in “Adaptive LL(*) Parsing: The Power of Dynamic Analysis” (2014) Parr, Harwell, and Fisher begins “Computer language parsing is still not a solved problem in practice, despite the sophistication of modern parsing strategies and long history of academic study.” They identify some of the same issues I’ll be discussing. However, I have a few additional concerns. In particular, I believe compiler error handling needs to be significantly improved. That is discussed at the end of this post.

As I said, I’m approaching the problem of parsing from the perspective of a programming language designer. There isn’t a single best parsing algorithm or parser generator for all use cases. My purpose is to lay out what I think a language designer needs from a parser generator. To a lesser extent, I also discuss DSLs. This means I’m not concerned with any of the following:

• parsing binary files
• parsing all existing programming languages
• parsing network streams
• parsing every strange grammar construction that might be possible
• parsing markup languages

Nice to Have

Before getting into what I see as the requirements for a parser generator for a language designer, let’s get out of the way those features that are useful but not necessary.

Composability

Many authors focus on the issue of composing grammars to form new composite languages. For example, by embedding SQL statements as queries in another language like Java. Alternatively, composability can be used for intermixing languages as when languages are combined with HTML to form webpage templates. It can also be useful for embedding DSLs with different syntax into a host language. Parser generators often have one or both of two problems with this. First, combining two context-free grammars that conform to the limitations of the grammars accepted by the tool may not produce a grammar that does. Indeed, in the general case, combining two unambiguous grammars may produce an ambiguous grammar. Second, generators dependent on a separate lexer aren’t able to combine their lexical specifications because the lexer often doesn’t have enough information to switch between the two languages as needed. The scannerless parser generators often tout the ability to handle combining grammars, but still suffer from the first issue.

While having a tool that supports combining grammars would be handy, I don’t see it as a must-have. In practice, languages are not combined very often. I don’t think that is because of challenges with the tools, but rather it is not a problem that comes up very often. When it does arise, it is not as much of a problem as claimed. If the languages being combined are radically different, then for the sake of the programmer, there will probably need to be unambiguous delimiters at the transitions between the languages. These can be used to write melded lexer and grammar specifications easily. More often what is being done is adding features similar to another language, as was done when adding LINQ to C#. It simply doesn’t make sense to combine languages with different rules for numeric or other tokens.

As I’ll discuss later, I find having a separate lexer valuable and don’t see the benefits to composability outweighing that. However, if it is possible to design tools with distinct lexing and parsing phases that enable or ease combining grammars, that would be wonderful.

Incremental Lexing and Parsing

As compilers and source code have grown in length and complexity, one response has been to adopt more incremental compilation. The ultimate in incremental compilation is to support incremental lexing and parsing. These enable advanced use cases like re-lexing and parsing as the developer types to provide real-time compiler errors. Out of the box support for incremental lexing and parsing would enable newly designed languages to offer these sophisticated features more easily. However, programmers have not yet come to see these features as mandatory for their work. New languages can afford to wait until they are mature to offer these.

Control of Error Parsing

I’ll discuss error handling in detail later. Here, I’d like to discuss a feature that might enable even better error handling but is definitely not required. In most compilers, the phases of compilation are independent so that information from later stages can’t influence earlier phases. For correct programs, this works fine. However, when source code contains errors, early phases are forced to attempt to diagnose and recover from errors without access to analysis from later steps. For example, a parse error might be resolvable by inserting tokens in one of two different ways. The parser must make an arbitrary decision between these two resolutions. It might be the case though that one of the two produces a well-typed syntax tree while the other does not. If it were possible to easily control the resolution of errors in the parser, it might be possible to use the type information to make the correct decision.

Token Value Generation

“Some Strategies For Fast Lexical Analysis when Parsing Programming Languages” discusses optimizing a lexer by generating token values during lexing. That is, since the characters are already being read once, create the value of a token during the initial lexing phase rather than reprocessing the token text after the fact. For example, compute the value of a numeric constant during lexing or generate the value of a string constant accounting for escape sequences. I’ve never seen a lexer generator that directly supports this (some can be fudged with lexer actions). The handling of escape sequences in strings has been particularly irksome to me. The lexer has already correctly identified each escape sequence, yet I end up writing a separate pass through the token value to generate the string constant which must also recognize the escape sequences. A similar operation is to compute the hash of an identifier during lexing and use it to perform string interning during lexing. This could entirely avoid the creation of many string objects.

Requirements

Having gotten some nice to have features out of the way, let’s look at what I consider to be the required features for a parser generator for programming language design. Throughout these, there are two recurring themes. First, languages that are being designed are in flux, and their grammars evolve over time. This is not always limited to simple additions and the designer may change to a radically different syntax or make fundamental semantic changes to the language. Second, error handling is essential. Besides generating correct, performant machine code, a compiler’s most crucial task is to provide high-quality error messages to the developer. The quality of error messages impacts language adoption and is the majority of the “user interface” of a compiler.

Separate Lexer

Scannerless parsing has grown in popularity as the increased performance of computers has made it feasible. As previously discussed, this is currently required for grammar composability. The lack of a separate lexer specification and attended specification language is often perceived as simplifying the use of the generator. However, I believe this is a tempting trap. As grammars grow, having a separate lexical specification begins to pay dividends. It gathers together the complete set of legal tokens rather than having them scattered throughout a grammar. Having a language designed specifically for lexing simplifies the specification. Without this, the somewhat distinct needs of lexing must be shoehorned into the formalisms of the parsing technology. Also, separating the lexer and parser doesn’t mean that fixed tokens like keywords and operators can’t be named by their text within the parser specification. Having a separate lexer is also valuable in implementing a number of the other requirements I will discuss.

Ultimately though, the argument for having a separate lexer is that it matches human language processing. People reading a text first separate it into tokens and then process those. Reflecting this two-layer scheme in the design of the language produces languages which are easy to read and simple to parse. Of course, there are instances where humans use top-down processing to adjust how they perceive individual tokens, but these are relatively rare. Likewise, there are instances where the parser providing input to the lexer is useful, but they are rare. These are better handled through specific lexer features. Many such cases can be dealt with through lexer modes and custom lexer actions. In other instances, this is not possible, but the parsing tool could be modified to better support it. Contextual keywords are a common example where separating lexing and parsing causes problems. However, this could be easily handled if a parser rule could specify that it matched an identifier with a particular value. Thus the lexer could emit contextual keywords as identifiers in all instances, but the grammar could express that certain words were expected in certain situations. Special handling for cases like the ambiguity between Java’s >> operator and generics could also be developed. String interpolation is another common situation that should be accounted for.

Unicode Support

Unicode support should go without saying. However, many parsing tools were developed before the widespread adoption of Unicode or support was left out to simplify the tool. Modern languages must provide Unicode support in strings if not also in identifiers. The challenge for parser generators is the vast number of states that Unicode support can produce. It can be a difficult performance issue for scannerless parsers. This is a situation where the separation of the lexer and parser can be advantages so that the complexity of Unicode can be isolated to the lexer.

Unambiguous Grammars

The limitations of LL and LR grammars have led to newer tools adopting algorithms that embrace ambiguity. That is they accept ambiguous grammars and either produce parse forests or report and resolve ambiguity at runtime. They trade the problems of limited grammars for the uncertainty of ambiguous grammars. As a language designer, one wants to know that their language parses unambiguously. There has been work on identifying ambiguity in fully general context-free grammars. However since detecting ambiguity is an undecidable problem, these approaches must by necessity be approximate. Besides which, most tools don’t offer any form of compile-time ambiguity detection anyway.

Since we can’t detect arbitrary ambiguity, what we need is a new class of grammars which are unambiguous, but flexible enough to include the kinds of grammars we would naturally want to write for programming languages. Perhaps, by setting aside the problem of efficient parsing and looking only at building up unambiguous grammars, we could find such a class of grammars. That way, we could verify the grammar to be in that unambiguous class. Then we could use an algorithm like Marpa, which while accepting ambiguous grammars claims to parse all reasonable unambiguous grammars in linear time, to implement the parser.

Flexible Grammars and Disambiguation

For a fully known and static language, adapting a grammar to the limitations of LL or LR parsing is painful, but doable. For an open-ended, continually changing language, it is too much work. Simple modifications to a grammar can break the limitations. For me, lack of support for left-recursion is a nonstarter. What a language designer needs is support for a relatively flexible set of grammars that allow them to worry about their language instead of satisfying the parser generator. Likewise, when operators may be added and removed, rewriting a grammar to encode precedence levels is onerous. The parser generator should provide simple ways of specifying operator precedence and associativity as disambiguation rules on top of the grammar.

Support Intransitive Operator Precedence

I’ve written before about how languages need to adopt intransitive operator precedence. When specifying disambiguation rules for operator precedence and associativity, this should be supported.

AST Generation and Control

When implementing the compiler for a new language, rapid development is vital. To support that, parser generator tools should provide automatic generation of abstract syntax trees. While not all designers may choose to use these, they can be an invaluable aid to those who do. To enable widespread adoption of these ASTs, they should be flexible in two ways. First in the structure of the generated tree and second in the actual code generated.

When using current parser generators, the AST often doesn’t match the structure of the grammar. Thus the grammar isn’t a reasonable basis from which to generate the AST. Support for flexible grammars and disambiguation should go a long way to mitigating this. However, more control over the generated AST could be invaluable. The Hime parser generator has a unique feature in this regard that more tools should adopt. Grammars can be augmented with annotations termed tree actions which allow for the modification of the AST produced. Additional grammar features like lists (which may be token separated) enable ASTs to reflect the desired structure rather than the limitations of BNF. They can also enable optimizations. For example, lists can improve on the performance of right-recursive grammars for lists in LR parsers. It should also be possible to control which tokens and location information is included in the AST.

Getting AST nodes written in a compatible style can be just as important as getting the right AST structure. Tools that do generate ASTs frequently provide little to no control over the code generated for those ASTs. This can lead developers to abandon the use of those ASTs or the tool altogether. Full AST node customization may not be in the cards, but a few options should be available. In particular, I’d like to see control over node mutability so that immutable, partially mutable, or fully mutable nodes could be used. It should also be possible to easily add properties to all or a given subset of nodes. For example, to add a data type property to all expression nodes which will later be set to the expression’s data type by the type checker.

Support Concrete Syntax Trees

Increasingly, the compiler is not the only tool that needs to lex and parse source code in a given language. Yet these tools are often forced to implement their own lexers and parsers rather than reusing the ones used by the compiler. The problem is that they need access not merely to the AST but to the concrete syntax tree. That is the syntax tree with every token and all whitespace and comments included. The concrete syntax tree enables tools like automated refactoring, pretty-printing, code linters and document comment generators. Parser generators should support the reuse of a single grammar in both the compiler and these tools.

Usability

As is too often the case with open-source tools, parser generators are often lacking in usability. Tools syntax, features, and limitations need to be clearly documented. They should be designed to be easy to learn and the grammars to be easily read. Remember that people using a parser generator are often using it for the first time and users referring to the grammar may not be familiar with the tool. Additionally, grammar errors should be clearly reported. Too frequently the error messages of parser generators are incomprehensible without detailed knowledge of the parsing algorithm being used. Sometimes, even that is not enough, and one must understand the particular implementation of the parser generator. Ambiguities and unsupported forms in the grammar should be clearly reported with an indication of which rules are the problem and where in the rule the issue occurs. The exact nature of the issue should be clearly explained. Ideally, an example string which will cause the parsing problem would be provided and if there is an ambiguity the different possible parse trees offered.

Performance

Performance still matters for generated parser even with today’s computers being multiple orders of magnitude faster than those available when parsing algorithms were first being developed. Developers still frequently complain about slow compilation times. The generated lexer and parser should be opportunities for easy performance wins as optimizations can be shared by every program using the tool. As one example, check out “Some Strategies For Fast Lexical Analysis when Parsing Programming Languages” which describes a detailed optimization of a lexer that achieves significant performance improvements over generated lexers.

While performance is important, there is an important caveat to that. For correct code lexing and parsing should be fast. That is, they should be linear with a low constant, ideally on par with LL and LR algorithms. The vast majority of code compiled parses without error. However, for code with parsing errors, performance is much less of a concern. In most situations, there is a single or a few files with parsing errors. In those cases, producing good compiler errors is more important than fast parsing. So much so that it may not even be unreasonable to parse the file again with a different algorithm that handles errors better.

Compiler Error Handling

I’ve saved the most important requirement for last. As I wrote above, generating good compiler error messages is one of the core responsibilities of a compiler. Yet, compiler generator tools give this short shrift. They often default to producing nothing but the first parse error and failing. That parse error is often confusing and poorly written. It refers to the particular convoluted grammar the tool happened to support. Reading the documentation on error handling often gives a short discussion of panicking (throwing away tokens) and of error rules. There is little to no discussion of how to generate the kind of good compiler errors developers expect from their compilers. Often the sample grammars have no error handling support. Many compiler tools provide virtually no information to use when trying to generate high-quality error messages. Furthermore, the very concept of compiler errors often seems to be a foreign concept to the tool, being totally omitted from the parser API.

Parser generators should make compiler errors a focus. They should provide lots of features for handling parse errors and detailed documentation on how to make the best use of those features. The default error messages generated by the compiler should be as good as possible for the programmer, not the grammar writer. Rather than offering minimal recovery strategies and hoping that the rest of the file will parse, the tool should fallback to a more sophisticated parsing strategy in the face of errors. One that can take into account parsing after the error to select the best recovery choice. This is an area where parser generators could offer a great deal of value over hand-written parsers. Very few hand-written parsers can afford a second parsing strategy optimized for error recovery. A parser generator can feed the single grammar into two different algorithms to offer this functionality with little to no impact to the compiler writer.

Enabling Language Growth

All of the requirements I’ve laid out here can be summed up by one goal: enabling language growth. That is supporting the life cycle of new languages by providing value in each phase of their development and building on past stages with each new one. Initially, a new language needs a quick and dirty way to get lexing and parsing working for a small grammar. Existing parser generators do ok at this but would benefit from AST generation and improved usability. As the language grows and evolves, support for flexible grammars and disambiguation enables rapid design iteration. Additionally, having a separate lexer and unambiguous grammars guide the language development toward good designs while support for intransitive operator precedence provides design freedom. As the language nears v1.0, Unicode support, performance and error handling become important. Then as the ecosystem matures, further improvements to error handling and the development of additional tools for the language ecosystem enabled by concrete syntax trees bring the language on par with the mainstream languages with which it is competing.

Requirements Summary:

• Separate Lexer
• Unicode Support
• Unambiguous Grammars
• Flexible Grammars and Disambiguation
• Support Intransitive Operator Precedence
• AST Generation and Control
• Support Concrete Syntax Trees
• Usability
• Performance
• Compiler Error Handling

Additional Reading:

• Parsing: a timeline by Jeffrey Kegler author of Marpa is a good history of parsing algorithms with a bias toward those leading to the algorithm used in Marpa. In particular, it omits GLL and GLR.
• What are the reasonable computer languages? by Jeffrey Kegler
• Parsing Expressions by Recursive Descent by Theodore Norvell
• Generating Good Syntax Errors (in LR parsers) by Russ Cox
• Parsing list comprehensions is hard by Michael Arntzenius
• A Haskell challenge by Jeffrey Kegler responds to “Parsing list comprehensions is hard” in the context of Marpa.

The longer I’ve thought about how to handle operator precedence and associatively in a programming language, the more convinced I’ve become that languages have fallen short. Because it was simple, easy and efficient, language designers have generally provided a total order for operator precedence and made all operators associative. This is typically expressed as a set of operator precedence levels and associativity for each operator. However, this often leads to unexpected or even confusing precedence between operators. Languages allowing programmers to define new operators from combinations of symbols are particularly hurt by forcing all operators to be placed in one of a few precedence levels. In reaction, some designers eschew operator precedence entirely. While simple, that violates deep-seated programmer intuitions opening the way for mistakes and surprise. I believe future languages should adopt intransitive operator precedence instead.

Note: I am focused here only on language with infix operators. Languages using prefix notation, such as Lisp variants, and languages using postfix notation, such as Forth, can be unambiguous without operator precedence.

Existing Practise

Most programming languages with infix operators fall into one of four categories:

1. Total Order Precedence and Total Associativity: Every operator has a precedence relative to every other operator. Every operator is either left- or right-associative.
   Example Languages: C, C++, C♯, Java, Go, Lua, Kotlin
2. Total Order Precedence with Partial Associativity: Every operator has a precedence relative to every other operator. Some operators are neither left- nor right-associative. In some languages, there are non-associative operators. For example, in Rust x <= y == z is illegal and would need to have parentheses added. In other languages, chained operators are interpreted differently. For example, in Python x < y < z is equivalent to x < y and y < z.
   Example Languages: Python, Rust, Prolog, Haskell, Perl
3. Single Precedence and Associativity: Every infix operator has the same precedence and associativity. Unary operators may or may not have higher precedence than binary operators.
   Example Languages: Smalltalk, APL, Mary
4. Single Precedence and Non-associative: Every infix operator has the same precedence and is non-associative. Thus all expressions must be fully disambiguated with parentheses. Unary operators may or may not have higher precedence than binary operators.
   Example Languages: occam, Pony, RELAX NG

Faults

Unfortunately, each these options has shortcomings. A set of test expressions best illustrates this.

• x + y * z is almost universally read as x + (y * z) because this is the convention everyone is taught from elementary school onward. Breaking this convention will only lead to confusion and frustration. Requiring explicit parentheses, in this case, isn’t as bad, but is still annoying.
• x < y < z is probably either a bug or meant to mean x < y and y < z. Treating relational operators as left-associative has led to hard to spot bugs in C code.
• By mathematical convention, logical-and has higher precedence than logical-or, so a or b and c should be parsed as a or (b and c). However, there is no convention for the relative precedence of logical-xor. Any precedence assigned to it will be arbitrary. Yet, all logical connective should have lower precedence than equality. Thus we need an operator that has no precedence relative to some operators, but precedence relative to others so that a xor x == y parses as a xor (x == y), but a xor b or c is an error.

Let’s consider how each of the approaches fairs on our test cases. Of course, we don’t want to evaluate a single language, but an idealized version of each approach. Single precedence and associativity requires that all operators be either left- or right-associative; which should we pick? Regardless of which is chosen, it will be easy to construct examples where it is incorrect for the operators involved. To simplify the test, I’ve always assumed the worst case for the given test.

Partial Order

Of the existing options, total order precedence with partial associativity scores the best. However, it fails to treat a xor b or c as an error. How can we fix this? Well, we could make operator precedence a partial order instead of a total order. We could then include in our precedence or ≺ and, xor ≺ ==, or ≺ ==, and and ≺ ==. That would correctly handle both a xor x == y and a xor b or c.

However, using a partial order for operator precedence can still lead to problems. Consider the expression x and y + z. Since this mixes logical and arithmetic operators, there isn’t an obvious precedence. We want to force the developer to add parentheses. One might think this is not a problem for a partial order. Yet, logical operators are lower precedence than equality (and ≺ ==) and equality is lower precedence than arithmetic (== ≺ +). Since partial order relations are transitive, those imply that and ≺ +. That isn’t what we want, so we need a precedence relation that is intransitive.

Intransitive Precedence

Let’s define the kind of precedence we want. I’ll call this an intransitive operator precedence. We’ll define both an equivalence relation “≐” for operators at the same precedence and a compatible order relation “⋖” for operators with different precedence. However, our precedence relation will be intransitive. Additionally, we’ll require that the precedence form a DAG. We can then use them to define the precedence relationships between our operators. Associativity will be specified separately.

For the mathematically inclined, the relations have the following properties:

1. ≐ is an equivalence relation:
   • a ≐ a (reflexivity)
   • if a ≐ b then b ≐ a (symmetry)
   • if a ≐ b and b ≐ c then a ≐ c (transitivity)
2. ⋖ is a strict intransitive order compatible with the equivalence relation
   • It is never the case that a ⋖ a (irreflexivity)
   • If a ⋖ b, then it is not the case that b ⋖ a (asymmetry)
   • If a ⋖ b and b ⋖ c, it does not follow that a ⋖ c (but it could be the case) (intransitivity)
   • There does not exist a₀ , … , a_n such that a₀ ⋖ a₁ , … , a_n-1 ⋖ a_n and a_n ⋖ a₀ (acyclic)
   • If a ≐ b and a ⋖ c, then b ⋖ c. Likewise if a ≐ b and d ⋖ a, then d ⋖ b.

This allows us to declare our desired precedence reasonably easily. First, we declare which operators have equal precedence, for example * ≐ /. Then we declare the relative precedence of operators, for example or ⋖ and. Operators of equal precedence share in the precedence we define. However, because precedence is intransitive, there can still be a lot of relations to specify. To simplify, we adopt two notational conveniences. First, that a precedence chain relates every operator to every other operator before and after it so that or ⋖ and ⋖ not states that or ⋖ not as well and second, that groups of operators can be related by using sets. For example, {and, or, not} ⋖ == relates all the boolean operators to the equality operator.

An Example

It’s easy to get lost in the math and notation. Let’s look at a concrete example to see how this might play out in a real language. Below I’ve defined a simple expression language over integers and booleans. To be clear, I’m not arguing for this particular set of operator precedences. Other language designers may prefer slightly different ones. I am arguing that languages should use this kind of flexible precedence to avoid undesirable precedence relationships.

I’ve used a form of EBNF augmented with additional notation to represent associativity and intransitive operator precedence. Without these additional annotations, the grammar would be an ambiguous expression grammar. The intent is that a hypothetical parser generator could directly use this grammar. The grammar notation section below gives a detailed explanation of the additional notation used.

(E) = "(" (E) ")"   #Parens
    (* Arithmetic Operators *)
    | (E) "+" E     #Add
    | (E) "-" E     #Sub
    | (E) "*" E     #Mul
    | E "/" E       #Div
    | E "^" (E)     #Pow (* raise to power *)
    | "-" E         #Neg
    (* Equality Operators *)
    | E "==" E      #EQ
    | E "<>" E      #NEQ
    (* Relational Operators *)
    | E "<" E       #LT
    | E "<=" E      #LTE
    | E ">" E       #GT
    | E ">=" E      #GTE
    (* Logical Operators *)
    | (E) "and" E   #And
    | (E) "or" E    #Or
    | (E) "xor" E   #Xor
    | "not" (E)     #Not
    (* Conditional Operator *)
    | E "?" E ":" E #Cond
    (* Variables *)
    | ID            #Var
    ;

ID = ?identifier?;

(* arithmetic precedence  *)
#Add =.= #Sub;

#Cond[inner, right]
    <. #Add
    (* division is not equal to multiplication *)
    <. {#Mul, #Div}
    (* negative exponent allowed *)
    <. #Pow[right]
    <. #Neg
    (* negative base requires parens *)
    <. #Pow[left]
    <. #Parens;

(* equality and relation precedence *)
#EQ =.= #NEQ;
#LT =.= #LTE =.= #GT =.= GTE;

#EQ (* following C convention, equality is below relation *)
    <. #LT
    (* equality and relation are below arithmetic *)
    <. {#Add, #Mul, #Div, #Neg, #Pow};

(* logical operator precedence *)
#Or <. #And;

#Cond
    <. {#Or, #Xor, #And}
    (* logical are below equality and relation *)
    <. {#EQ, #LT}
    (* both are below logical not *)
    <. #Not
    (* all lower than parentheses *)
    <. #Parens;

This grammar tries to follow mathematical conventions without relating operators that have no conventional relationship. Powers are right associative and higher precedence than negation. The division slash is non-associative to avoid confusion. It does follow the C convention and make equality lower precedence than relations. The test cases below demonstrate the grammar has the desired properties.

Added Grammar Notation

In the grammar above (E) = indicates that E is a “parenthesized” nonterminal. Normally, the declaration of E would be ambiguous, but a parenthesized nonterminal defaults to disallowing alternatives containing recursive uses of the nonterminal from being immediate children of the production. Thus (P) = P "~" P | P "$" P | ID; is effectively transformed to P = P' "~" P' | P' "$" P'; P' = ID;. This has the effect of making the operators non-associative. The intuition here is that parenthesized nonterminals will have to be fully parenthesized unless additional associativity and precedence rules are declared.

Associativity is indicated by enclosing a recursive use of the nonterminal in parentheses. A recursive use enclosed in parentheses allows the same alternative to occur as a direct child of that nonterminal. Thus (E) = (E) "+" E is left-associative and (E) = E "^" (E) is right-associative. The rule (P) = (P) "~" (P) is ambiguous. Again, non-associative is the default for parenthesized nonterminals, i.e. (E) = E "<" E. Intuitively, the parentheses indicate which side expressions should be grouped on. One wrinkle this creates is that to allow nesting of parentheses in parentheses, the nonterminal must be enclosed in parentheses as (E) = "(" (E) ")" or else ((x)) is illegal.

Labels are applied to each alternative by placing them after the alternative. Labels are prefixed with a pound sign. The ANTLR parser generator uses the same notation. Labels provide a way to refer to alternatives later. They can also be used by a parser generator to name the AST node for that alternative.

Operator precedence is declared after the production rules using the precedence relation applied to the alternative labels. Using the labels makes it easy to give binary and unary versions of the same operator different precedences. Two operators are given the same precedence using the =.= operator. Relative precedence is established using the <. operator. As described in the previous section, chains and sets can be used to simplify the declaration of precedence. A precedence declaration affects recursive uses of the nonterminal in the alternatives it relates. Alternatives with higher precedence may be direct children at any use of the nonterminal. Alternatives with equal precedence may only be direct children where the nonterminal is enclosed in parentheses.

In some instances, more complex operators have different precedence for different subexpressions. An array indexing operator (P) = P "[" P "]" #Index; would be such a situation. Here, the bracketed P could be of any precedence while the left P must be higher precedence. In such situations, we can refer to the precedence of the subexpressions using a bracket notation listing the indexes of nonterminals in the alternative. For example, #Index[1] refers to the first subexpression, #Index[2] refers to the second, and #Index[1,2] refers to both. For convenience, four shorthands are provided. The names left and right refer to the leftmost and rightmost nonterminal not bracketed by a terminal. In the example, #Index[left] is the same as #Index[1] while #Index[right] is an error because the rightmost P has the terminal "]" to its right. The name outer refers to both the left and right so #X[outer] would be equal to #X[left, right]. The name inner refers to every subexpression that is not an outer subexpression. Thus #Index[inner] would be equal to #Index[2]. In the example grammar above, this is used to allow a negative sign in the exponent while giving exponentiation higher precedence and to allow logical but not arithmetic expressions in the condition of a conditional expression.

Don’t Mix Associativity

To consider the issues involved in mixing operators with different associativity at the same precedence level, imagine adding the following to the above grammar.

(E) = (E) "⊕" E  #CAdd (* left-associative *)
    | E "⍟" (E)  #CPow (* right-associative *)
    | E "⊜" E    #CEQ  (* non-associative *)
    ;

#CAdd =.= #CPow =.= #CEQ;

By the rules stated before, what would the effect of this be? Let’s look at each case.

Given that this is almost certainly not what one wants, it is best to simply make it illegal to have operators with the same precedence but different associativity.

Assignment Example

In C style languages the assignment operator is right-associative and evaluates to the value of the left-hand variable after it is assigned. Assignment has lower precedence than addition, so the expression a+b=c+d parses to (a+b)=(c+d) which is illegal. One might prefer that it parse as a+(b=(c+d)). Setting aside whether that is a good idea, it can be achieved with this scheme. The example expression grammar could be extended with assignment by adding the rule and precedences below. By splitting the precedence of the left and right, we can make assignment bind very tightly on the left, but very loosely on the right.

(E) = E "=" (E) #Assign;

{#Cond, #Add, #Mul, #Div, #Pow, #Neg,
        #Or, #Xor, #And, #Not, #EQ, #LT}
    <. #Assign[left];

#Assign[right]
    <. {#Cond, #Add, #Mul, #Div, #Pow, #Neg, #Parens,
        #Or, #Xor, #And, #Not, #EQ, #LT};

What Now?

I’m not the first one to propose something like intransitive operator precedence. The Fortress language has an elaborate operator precedence scheme that is similar. Check out The Fortress Language Specification v1.0, chapter 16 for more information. However, it was difficult to find much else. The precedence level approach seems to have completely dominated. Hopefully, I’ve convinced you of the value of intransitive operator precedence or at least given you something to think about. I’d love to see future programming languages adopt this approach. Unfortunately, algorithms for parsing such precedence schemes are lacking. If you want to implement such a scheme or are interested in learning more, check out these sources:

• Parsing Fortress Syntax by Sukyoung Ryu.
• Parsing Mixfix Operators by Nils Anders Danielsson and Ulf Norell which proposes a similar scheme for the Agda language.
• SDF and SDF3 which provide both position based priority and intransitive priority for parsing.

Many people have had the idea that there should be a way to visualize lifetimes in Rust. Indeed, the Rust Book used to include ASCII diagrams of lifetimes in some code examples. When fighting the borrow checker, it would be great if the IDE or editor could automatically provide a visualization of the lifetimes in your code. Perhaps the most beautiful visualization I have seen is in the post “Graphical depiction of ownership and borrowing in Rust” by Phil Ruffwind. However, those diagrams take up a lot of space. Some of the code samples have blank lines inserted in them to allow space for the diagram. They aren’t well suited to use in an IDE or editor. However, others have already worked on editors to visualize Rust lifetimes.

Paul Daniel Faria has developed a prototype plugin for the Atom editor that provides lifetime visualizations. There is a long thread on the Rust Internals Forum discussing it. Several people propose variations on how the visualizer should work. The current approach is to select a variable and then visualize the lifetimes and borrows based around that variable. Highlighting similar to selections are used to show the code regions of borrows. The last screenshots provided show the visualization of the lifetime of the target3 variable and then the message variable in the same code sample.

I find these visualizations to be challenging to interpret. The highlighting style isn’t clear enough and is awkward when a single wrapped line is highlighted as with lines 52 and 53 in the first example. I understand this style was probably chosen because it is easy to implement in the Atom editor and I don’t fault the developer for starting there. Also, the fact that lifetimes are visible relative to only a single selected variable is very limiting. Finally, this prototype was done before the addition of non-lexical lifetimes (NLL) to Rust, and it isn’t clear how to adapt it for that. Given these issues, I wanted to imagine what I’d ideally want from an editor in the way of lifetime visualization.

I started with the diagrams in the “Graphical depiction of ownership and borrowing in Rust” post. However, as I said, they are too large to fit in an editor next to real-world code. I took screenshots from (VS Code) and used image editing software to mock up my ideas. After a few iterations, I came up with something that I think could be a good start. By way of example, here is what a simple method could look like:

The blue line shows the lifetime of the immutable variable x. The value comes into existence on line 9 as indicated by the blue circle. The variable continues to be live and accessible until the end of the block as indicated by the solid blue vertical line. At the end of the block, the value leaves scope and is dropped as indicated by the blue horizontal bar that terminates the lifetime line.

On line 10, the variable y borrows an immutable reference to x. The green lifetime line represents the reference y. It comes into existence on line 10 as a borrow of x as represented by the green circle around the blue circle that is connected to the lifetime line of x. Values are distinguished from references by use of hollow/double lines instead of solid. Since y immutably borrows x, it is still valid to read from x after it is borrowed. Thus there is no change to the blue line on line 10. Line 12 is the last use of y. Because of NLL, the lifetime of y ends here. However, it would be valid to add lines after this that use y. This is indicated by the thinning and transparency of the yellow line from here to the end of the scope.

That is a trivial example. It didn’t show mutable values or the locking and freezing of variables when they are borrowed. The example below demonstrates how those might be represented.

Here, the squiggly or wavy lines represent mutability of values/variables on that line. Thus x starts mutable. However, when it is mutably borrowed by y on line 19, it is locked, and x can no longer be accessed as long as it is borrowed. The thin dashed line represents this. On line 21, z immutably reborrows y. This causes y to become temporarily immutable which means it is now safe to read from x as indicated by its transition to a think solid line. Line 21 is the final use of y and line 22 is the final use of z as represented by the narrowing and transparency of their lifetimes.

These mockups show that it is probably possible to create a lifetime visualization that can be automatically generated by a source code editor and displayed inline with the code. However, these are limited, minimal examples. A full visualization feature would require accounting for many more situations. These would include:

• Moves can be represented similarly to how they are in the graphical depiction by replacing the lifetime line of one variable with another.
• Copies can be represented similarly to how they are in the graphical depiction by forking the lifetime line of a variable into a new variable.
• Parameters might be represented by lifetime lines that start before the function and end after it.
• Lifetime Annotations could be color-coded to match the lifetime line corresponding to them. Additionally, it might be possible to label the line with the lifetime name (for example 'a).
• Nested Functions can probably be treated similarly to regular functions, though there may be issues with the lifetime lines of values that span over the nested function definitions.
• Closures will require careful consideration to account for both closure parameters and captured values. Remember that variables can be captured both by borrowing and by taking ownership.
• Struct Fields may pose additional problems since they could be borrowed or moved separately from the containing structure.
• Temporary Values may also need to be represented somehow.

There may be better ways of visually representing lifetimes and their relationships than this. In particular, the following should be considered:

• Is there a way to better connect variable uses to the lifetime visualization? I considered color coding variables to match their lifetimes, but that might mix poorly with standard syntax highlighting.
• Should there be a visual distinction between a no-op drop vs. ones that have an actual drop function? Remember that the call to drop counts as a use of the variable for NLL.
• Is there a better way to represent NLL? An earlier iteration of my mockups had the lifetime lines fading away after the last line they were used on. That produced cleaner diagrams, but it was unclear how long variables remained accessible. One idea is to mark the ends of blocks with horizontal white bars. Thus a NLL would fade out at last use, but following the column down to the first white bar blocking the column would indicate the last line the variable could be used on.
• How should the forthcoming async/await features in Rust affect the lifetime visualization?
• If there are errors in the lifetime relationships, how can these be indicated in a way that makes the issue clear?
• Is there a better way to associate borrows with the value they are borrowing? Currently, a borrow only gives an indication of which value it is borrowing on the first row. In an earlier iteration of the design, the color of the borrowed value continued down the middle of the reference lifetime. I wasn’t able to make that look good, but perhaps a graphic designer could come up with something better.
• Will the visualization remain useful for long or complex functions? In particular, there might be many columns for a function with many variables. Ideally, columns could be reused for different variables after the last use of a variable. However, that interferes with indicating the entire scope a variable might be usable in. There may need to be special handling for such situations. Perhaps the lifetime lines of multiple variables can be collapsed into a single column in certain circumstances.
• Should there be a change to the visualization when a variable is selected? It may be useful to show additional information about connected lifetimes when a variable is selected or to highlight the relevant portions of the visualization. Alternatively, perhaps the main visualization should be simplified and some information shown only when a variable is selected.
• Is there some radically different visualization that would be better?

I’d like to see great tools for Rust development. The Rust Language Server project is a good step in that direction. However, Rust tools would benefit from unique features not supported by the standard language server protocol such as the lifetime visualizations I’ve mocked up. Unfortunately, it appears that VS Code will not allow a plugin to add this kind of visualization unless it completely takes over rendering and editing of the source code. It is likely other editors will be restricted like VS Code. However, I think the Atom editor would allow a plugin to do this. Yet, these diagrams don’t seem well suited to generation with the HTML and CSS that Atom is built on. Given the challenges of implementing a visualization like this, it is unlikely I’ll ever implement it. I invite others to take my ideas and create great Rust tools.

EDIT 2019-02-21: Added bullet item about accounting for async/await features.